From epidemic spreads to flow in porous media, directed percolation provides a classic framework to model spreading patterns in networks. I am interested in how the classic invasion percolation framework is modified in more complex applications.
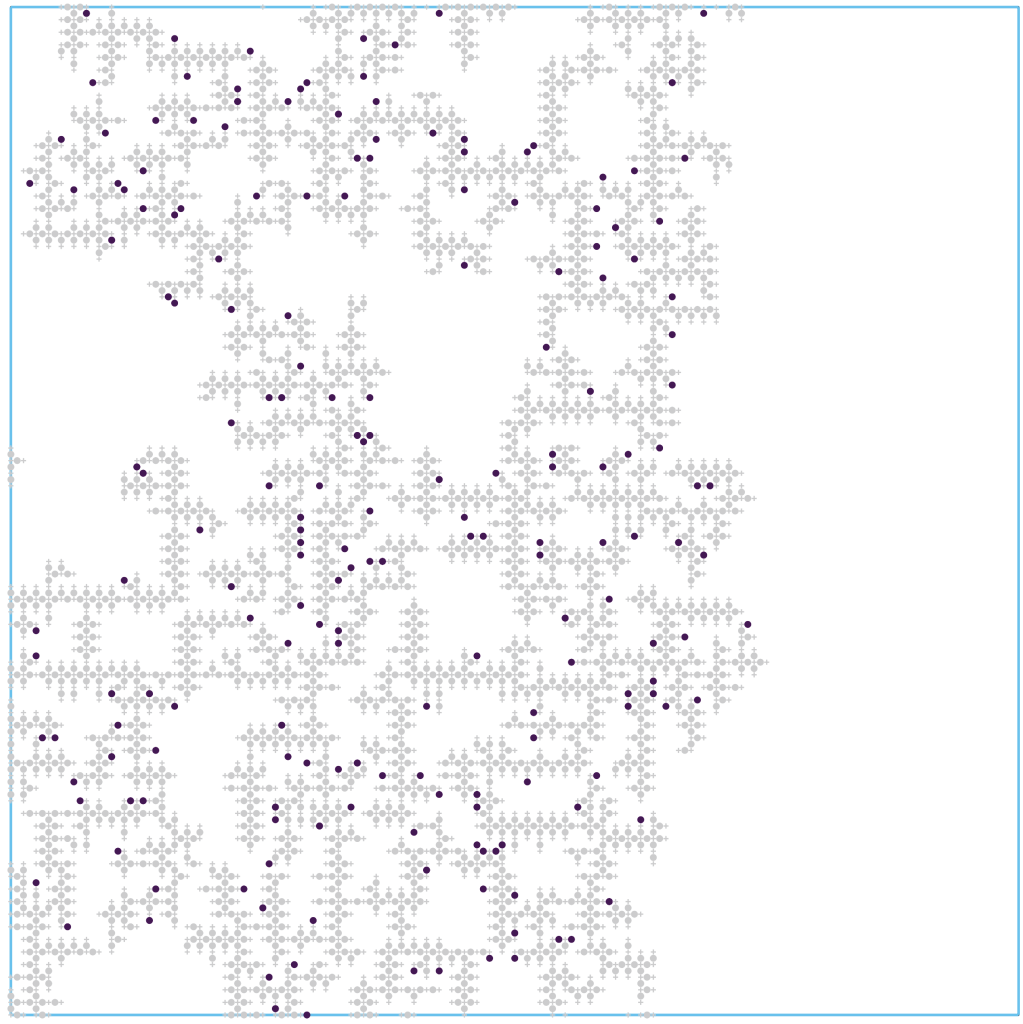
Dynamic “erosion percolation” in during fluid drainage in erodible porous media
Drainage, in which a nonwetting fluid displaces a wetting fluid from a porous medium, is well-studied for media with unchanging solid surfaces. However, many media can be eroded by drainage, with eroded material redeposited in pores downstream, altering further flow. Here, we use theory and simulation to examine how these coupled processes both alter the overall fluid displacement pathway and help reshape the solid medium. We find two new drainage behaviors with markedly different characteristics, and quantitatively delineate the conditions under which they arise. Our results thereby help expand current understanding of these rich physics, with implications for applications of drainage in industry and the environment.
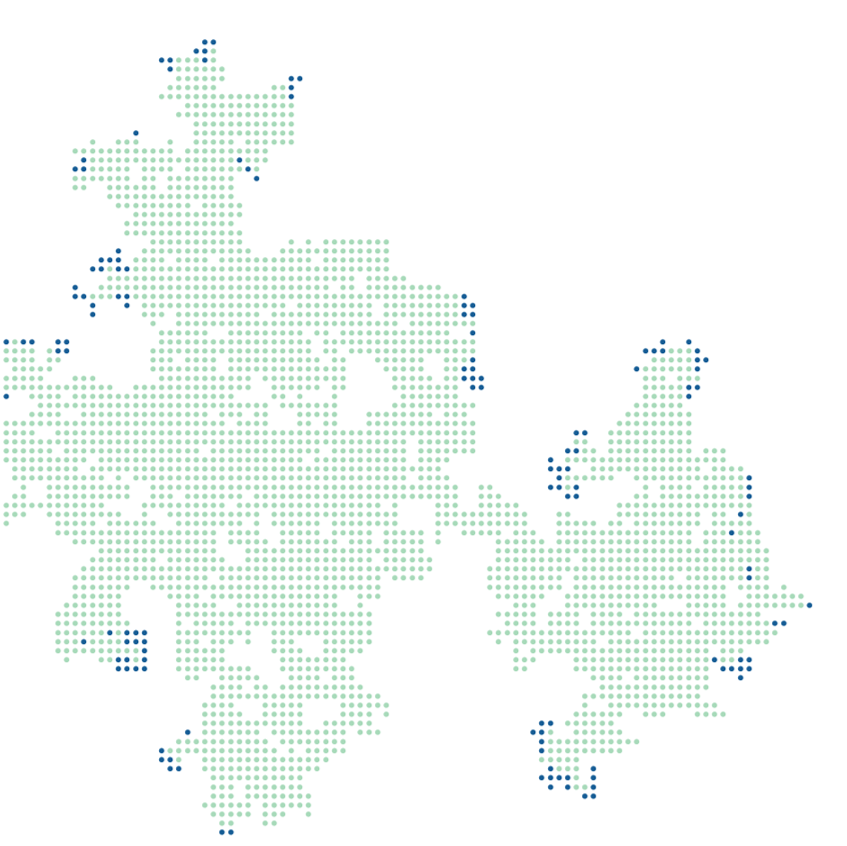
Dynamic “infection percolation” during epidemic spreading in social networks
Spatial percolation simulations are frequently used to analyze disease spreading in social networks in conjunction with time-based SIR models. We provide a simple framework to incorporate time-dependent spreads in a modified percolation algorithm, providing insights for how epidemics spread in space and time in simple networks. In social networks with heterogeneities, like near the boundary between communities with different health care access, the spread can be either exacerbated or quelled. We anticipate this novel framework can inform real epidemic policy decisions when implemented on more complex social networks.

Capillary fingering in gradients
Capillary fingering explains the process where a nonwetting fluid displaces a wetting fluid in a porous network: for example, oily contaminants trickling into a groundwater aquifer. Percolation describes this process well for homogenous media, but we showed experimentally that the predicted fingering pattern is modified starkly when the porous medium has spatial structure like pore size gradients, which are often found in real aquifer systems. Through simulations and theory, we explain how the modified fingering pattern depends on the relative magnitudes of the gradient along the flow direction and the disorder transverse to the flow direction.
